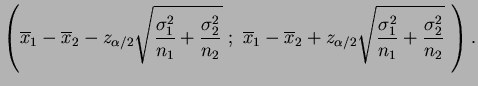Explicações Ensino Superior (Matemática)

Explicações de Matemática em Braga

 

Que tal entrar em Setembro a planear o próximo ano letivo?

Explicações de Matemática em Braga (Largo Senhora-a-Branca)

 

 

Distribuição t Student

Distribuição t

       Intervalos de confiança e testes estatísticos para comparação de médias são baseados na distribuição t. Esta distribuição é também chamada “t student”.

        A distribuição t é semelhante à distribuição Normal: simétrica em relação à média (0) mas com um desvio padrão dependente de um parâmetro chamado graus de liberdade.

 

A distribuição t é mais achatada que a Normal e à medida que o número de graus de liberdade aumenta, vai-se aproximando da Normal.

 

Testes de hipóteses - Tomada de decisão

Voltando ao assunto abordado num post anterior, a tomada de decisão em testes de hipóteses tem que ser de acordo com a região definida pelas hipóteses.

 

Assim:

 

 

 

Hipóteses estatísticas

Uma hipótese estatística é uma conjetura sobre a distribuição de uma ou mais populações.

 
Num teste de hipóteses são definidas:

       H₀ : Hipótese nula (hipótese da qual se parte)

H₁ : Hipótese alternativa (hipótese que se julga verdadeira e se pretende verificar)

Há três tipos de testes:

 

 

Regra de decisão estatística:

 

Princípio que determina a conclusão de rejeitar ou não rejeitar H_0, a partir da estatística de teste e do(s) valor(es) crítico(s).

            - Rejeitar H₀ : significa que os dados observados permitem concluir H₁ em detrimento de H₀

            - Não rejeitar H₀ : significa que não há evidências suficientes para rejeitar H₀  

 

 

 

 

 

 

 

 

 

 

Tipos de erros em Estatística

Tipos de Erro:

Erro tipo I e Erro tipo II

Diagrama de caixa e fio

O Diagrama de caixa e fio, também conhecido por Boxplot ou Diagrama caixa de bigodes é um gráfico muito útil para representar variáveis de natureza ordinal ou quantitativa.

 

Um exemplo:

Estimação por intervalos

Na estimação por intervalos, em vez de se indicar um valor concreto para certo parâmetro da população, constrói-se um intervalo, que com certo grau de certeza previamente fixado, contenha o parâmetro em causa.

 Estes intervalos, denominados intervalos de confiança, permitem assim medir a precisão de um estimador.

Podem construir-se I.C. para qualquer parâmetro da população.

Para construir um intervalo de confiança é necessário encontrar um estimador pontual, estabelecer um nível de confiança igual a 1- α , conhecer a dimensão da amostra e conhecer a distribuição do estimador. A α dá-se o nome de nível de significância.

Os níveis de confiança mais utilizados são 0.90, 0.95 e 0.99.

Distribuições teóricas discretas

As distribuições teóricas (quer elas sejam discretas ou contínuas), não são mais do que modelos matemáticos, mais concretamente, modelos probabilísticos, que se ajustam ao comportamento aleatório de alguns fenómenos do nosso dia-a-dia.

 

 

Distribuições discretas

 

Distribuição Uniforme

       Uma variável aleatória discreta tem Distribuição Uniforme, X~ Un (n), se todos os valores da variável aleatória têm a mesma probabilidade de ocorrer.

 

Distribuição Binomial

 

Considere-se uma prova de Bernoulli e uma variável aleatória X que só assume dois valores: o valor 0 quando o resultado da prova é o insucesso e o valor 1 quando o resultado da prova é o sucesso. Ao sucesso está associado a probabilidade p e ao insucesso a probabilidade q = 1-p, fixas.

 

A distribuição Binomial parece estar associada à seguinte questão genérica: qual a probabilidade de, em n provas de Bernoulli, serem obtidos x sucessos (a realização de certo acontecimento A) e portanto (n-x) insucessos (a não realização de A ).

 

 

Distribuição de Poisson

 

A distribuição de Poisson permite assim descrever certos tipos de fenómenos ou acontecimentos cuja ocorrência se repete ao longo do tempo ou do espaço (isto é, num espaço contínuo).

 

Teorema do Limite Central

O Teorema do Limite Central é um dos teoremas mais importantes da Estatística.

 

Genericamente, o Teorema do Limite Central (TLC) diz que a média de um grande número de variáveis aleatórias independentes tem uma distribuição que se aproxima à Normal.

 

As estatísticas das redes sociais

O papel da Estatística na Ciência

Estatísticas no feminino

O que as estatísticas revelam acerca do Twitter?

Estatística Inferencial

 

        A estatística descritiva mais não é que métodos a que se recorre para sumariar informação (diagramas, gráficos, estatísticas, …).

        Todavia a Estatística é mais que a recolha e apresentação de dados. A Estatística é uma ciência de tomada de decisões …

       A partir da análise de informação recolhida é possível tirar conclusões sobre a população da qual a amostra foi retirada.

       

        Em Estatística é fundamental distinguir se estamos a tratar informação relativa a uma amostra ou a uma população.

        Numa população as medidas de tendência central e de variação são fixas e invariantes, são características da população e têm o nome de parâmetros.

        Numa amostra estas medidas são estimativas e têm o nome de estatísticas.

                OBS: para distinguir estas medidas usam-se letras gregas para os parâmetros da população e letras latinas para as estatísticas amostrais.

O processo inferencial – tomada de decisões – é baseado em métodos estatísticos de estimação:

                - Estimação pontual: com base na informação amostral é produzido um valor para um determinado parâmetro da população

                - Estimação intervalar: é construído um intervalo que, com um certo grau de certeza, contém o verdadeiro valor do parâmetro da população

               

               - Estimação por testes de hipóteses: determinadas hipóteses sobre os parâmetros de uma ou mais populações são ou não validadas

Amostragem não aleatória

      Uma amostra não aleatória é uma amostra na qual se desconhece a probabilidade de um elemento da população ser escolhido para a integrar.

       Pode resultar de:

• Amostragem por conveniência
• Amostragem por quotas

 Amostragem (não aleatória) por conveniência

       Ocorre quando a participação é voluntária, acidental ou os elementos da amostra são escolhidos por uma questão de conveniência (muitas vezes, os amigos e os amigos dos amigos).
       Este processo não garante que a amostra seja representativa.
       Pode ser usada com êxito em situações nas quais seja mais importante captar ideias gerais, identificar aspetos críticos do que propriamente a objetividade científica.
       Vantagem: processo rápido, barato e fácil.

 

Amostragem (não aleatória) por quotas

        Análogo ao método de amostragem estratificada, mas em vez de se escolher uma amostra aleatória dentro de cada um dos estratos da etapa final, escolhe-se uma amostra não aleatória de tamanho determinado pela fração de amostragem.
         Desvantagens:
         - há quase sempre um enviesamento na seleção dos casos dentro dos estratos porque a amostra é normalmente escolhida por meio de um método de amostragem por conveniência.
        - não é possível extrapolar com confiança para a população os resultados e conclusões tiradas a partir da amostra.

Amostragem aleatória

 

Uma amostra aleatória é uma amostra na qual cada elemento da população tem a mesma probabilidade de ser incluído.

Pode resultar de:

      ·         Amostragem aleatória simples

·         Amostragem sistemática

·         Amostragem estratificada

·         Amostragem agrupada

 

Amostra aleatória simples

As duas maneiras mais utilizadas de obter a amostra de dimensão “n” são:

 - o método de sorteio, no qual são escolhidos um a um até que esteja completa a amostragem

 - a tabela de números aleatórios, na qual serão sorteados até que seja satisfeita a solicitação da amostra.

 

Amostra aleatória sistemática

É constituída por todos os elementos da população, selecionados de k em k elementos.

O valor de k obtém-se dividindo o número de elementos da população a amostrar pela dimensão da amostra.

Desvantagem: no caso de existir uma “periodicidade” escondida, perde-se o carácter aleatório pretendido.

Utiliza-se quando a população pode ser subdividida num conjunto de subpopulações ou estratos homogéneos.

Em cada estrato, selecionar uma amostra aleatória simples.

Estes estratos são normalmente formados por características naturais(escalões de idade, género, profissão, etc).

 

Amostra aleatória agrupada/conglomerada/ por clusters

Resulta de um processo em duas fases: num primeiro momento a população é dividida em subgrupos, num segundo momento é feita uma seleção aleatória  de elementos desses subgrupos da população.

Habitualmente os subgrupos são definidos pela área ocupada num mapa (distritos, concelhos, etc)  pelo que é útil em estudo de âmbito populacional/geográfico.

Desvantagem: processo menos eficiente que os anteriores, requerendo normalmente uma maior dimensão amostral.

Amostra e população

Uma amostra é um subconjunto da população selecionado de tal forma que seja representativo da população.

A importância da estatística inferencial é permitir a generalização dos resultados obtidos numa amostra para a população a da qual ela é retirada.

Tendo em conta que um dos principais objetivos de uma investigação é inferir da amostra para a população, existem vários métodos para a seleção de uma amostra que permita fazer essa inferência estatística (a tratar brevemente)

Razões para estudar uma amostra e não a população:

-              processo mais rápido

-              menos dispendioso

-              Impossibilidade do estudo da totalidade da população

A importância de saber interpretar o que nos diz a Estatística

10 estatísticas surpreendentes acerca dos social media

10 SURPRISING SOCIAL MEDIA STATISTICS THAT WILL MAKE YOU RETHINK YOUR SOCIAL STRATEGY

 

Investigação empírica

         

           Para estudar um fenómeno é feito um tratamento numérico das observações desse mesmo fenómeno – Quantificação – através da medição de variáveis, estimação dos parâmetros a partir da amostra e testes estatísticos.

            A Investigação Empírica é um tipo de estudo onde se fazem observações para compreender melhor o fenómeno a estudar. Permite construir explicações e/ou teorias mais adequadas, com base em dados reais e empíricos, estando por isso na base da investigação em Ciências Naturais e Sociais.

      

Há três tipos de investigação empírica:

·         Investigação Pura

Objetivo: descobrir factos novos para testar deduções feitas a partir de teorias que no momento da investigação parecem não ter aplicação prática (contribuindo assim para o conhecimento teórico).

·         Investigação Aplicada

Objetivo: descobrir factos novos para testar deduções feitas a partir de teorias que possam ser aplicadas a médio prazo.

 

·         Investigação Aplicável

Objetivo: descobrir factos novos que possam ser aplicados a curto prazo.

            A investigação empírica exige a definição de objetivos (para enriquecer o conhecimento), escolhas (tema e hipóteses a testar), planeamento (método para a recolha de dados) e pensar adiante (planear a análise dos dados antes da investigação empírica).

Software estatístico SPSS

SPSS - Statistical Package for the Social Sciences
 

O software estatístico SPSS é um poderoso sistema de análises estatísticas que permite manusear os dados através de menus e caixas de diálogo. O seu início remonta aos anos 60.

       Este programa permite uma análise estatística completa dos dados, através de métodos de Estatística Descritiva simples até processos de análise multivariada mais complexos.

 

Estatística

 
Estatística é um conjunto de métodos e técnicas destinadas ao estudo de populações, para a interpretação da realidade e para a previsão com base nessa realidade.

Objeto da Estatística extrair informação dos dados, os quais são muitas vezes incompletos, de forma a obter uma melhor compreensão das situações que representam.

 

Utilidade da Estatística:

 

—Descrever e compreender relações entre as variáveis: a quantidade de informação recolhida cresce tão rapidamente que se torna imprescindível tomar decisões corretas.

—Tomada de melhores e rápidas decisões: como a informação disponível está geralmente associada a um elevado grau de incerteza, a estatística fundamental para tirar conclusões válidas a partir de informação incompleta.

—Necessidade de planear as acções a empreender no futuro: donde a importância dos métodos estatísticos de previsão de acontecimentos futuros medindo as variações actuais e estabelecendo os cenários futuros mais prováveis.

O que nos dizem os dados?